SLIC超级像素分割算法的原理与实现+文献综述(5)
时间:2018-03-09 21:12 来源:毕业论文 作者:毕业论文 点击:次
1.2.2 基于梯度上升的方法 基于梯度上升的超级像素分割算法的基本思想是:从一个初始的粗糙的聚类开始进行迭代过程,每次迭代从先前的迭代结果中提炼出一个更好的分割,直到结果收敛为止,最终完成对图像的分割。 1.2.2.1 Watersheds方法 分水岭方法(以下简称WS91)用拓扑地形图来描述一幅图像,当应用于图像分割时,图像中每个像素的灰度值表示该点的海拔高度,每个局部极小值及其影响区域为集水盆,而集水盆的边界就形成了分水岭,大致模型可用图1.1描述。 1.1 分水岭示意图 分水岭分割算法借鉴了数学形态学的理论知识,最初由Digabel等人[23]将分水岭算法引入到了二值黑白图像的分析过程中。比较经典的计算方法是Vincent等人[15]提出的,采用了浸没算法的实现方案,将分水岭计算分为排序过程和浸没过程。 分水岭算法的优点是简洁、复杂度低O(NlogN)、运行时间短,且提取出的物体边缘轮廓线是封闭的,能准确定位目标物体。但是它也存在一定的缺点,分水岭分割会得到成千上万的集水盆,结果很细致,导致图像出现非常严重的过分割现象。 1.2.2.2 Mean shift方法 Comaniciu等人提出的Mean shift[16](以下简称MS02)提出了一种无参数的、基于核密度梯度估计的快速统计迭代算法。其基本思想是在核窗口依次计算所有特征空间数据点的mean-shift矢量,沿着mean-shift梯度上升方向移动,直到收敛到密度最大处,如图1.2所示。通过有限次迭代计算,能够快速找到数据分布的稳定点,即模点。利用MS02做图像分割,就是把具有相同模点的像素聚类到同一超级像素中的过程。 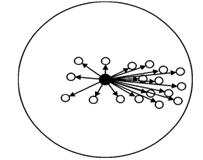 1.2 Mean shift示意图 MS02是一个迭代模式搜索的过程,它能产生形状规则的超级像素,但速度慢(复杂度为O(N2)),并且不能控制超级像素的数量、大小和紧凑度。MS02方法在实际应用中具有较好的稳定性和抗噪性,但由于分割时缺少图像语义信息,分割效果不够理想,存在过分割问题。 1.2.2.3 Quick shift方法 Vedaldi等人提出的Quick shift[17]分割算法(以下简称QS08)类似于MS02的模式搜索,但是比MS02快。它不断促使像素特征空间中的每一个数据点,向着能使Parzen密度估计增大的最近的像素移动来实现图像的分割。QS08算法是非迭代的,不能明确地控制生成超级像素的大小和数量,同时也非常速度也非常慢(复杂度为O(dN2),d为一个小的常数)。QS08已被应用于目标识别[9]和运动分割[24]。 1.2.2.4 Turbopixels方法 2009年Levinshtein等人提出的Turbopixels[18]方法(以下简称TP09),描述了一种基于几何流的水平集方法,能快速地产生超级像素。几何流依赖于局部图像梯度,目的是在图像平面上平均的分配超级像素。它们通过膨胀初始化种子点,并结合曲率演化模型和背景区域的骨架化过程,将图像分割为网格状的超级像素。 TP09是基于可变化复杂度的算法,但在实践中,根据作者的说法,复杂度近似为O(N)。但在实际表现中,TP09是最慢的算法之一。并且,TP09生成的超级像素过于规则和紧凑,使得它对图像边界保持的相对不好。 Xiang等人[25]提出从待分割的图像中构建多文特征图像的方法,应用于Turbopixel框架超级像素分割中。Cigla等人[26]介绍了一种快速的Turbopixel高效图论分割方法,先采用快速Turbopixel算法把图像分割为超级像素,再建立加权图,用Ncut算法得到图的最终分割结果。 1.3 本文的安排 第1章,首先给出本课题研究的背景和意义,简明扼要的介绍了超级像素的基本概念,描述了介绍SLIC算法的意义;并且对于超级像素生成算法的研究现状进行介绍,讨论了现有的几种超级像素算法。 (责任编辑:qin) |