将电场旋度方程代入式(2.2.4)，结合 ， 可得
             (2.2.5)
式中，J为分界面上棱边元的面电流，e为分界面上棱边元的电场。
以 为测试基函数，对式（2.2.1）作伽辽金变换，并将（2.2.5）代入其中；
以 为测试基函数，对式(2.2.5)做伽辽金变换，可得第 个区域的微分控制方程组：
                        (2.2.6)其中：
式中， 为第 个区域的系数矩阵， 为第 次求解得到的第 个子域内部边上的电场值以及分界面上内部边的电场值和电流值， 为初始的右边向量， 为相邻两个区域 与 的耦合矩阵， 表示本区域 和相邻区域 第 次求解到的分界面上内部边电场值的平均值和电流值的平均值， ， ， 分别是分界面位于自由空间时的耦合矩阵， 为区域内部的电场， 为区域分界面上的电场， 为有限元部分的矩阵，形式不变。
对于式(2.2.6)求解：
                        (2.2.12)
即先求 的逆矩阵，并对 的逆矩阵在内部使用直接解法，在外部用Gauss-Seidel迭代解法加速迭代：在每次迭代过程中，子域的电场电流和相邻子域在分界面上上一次迭代算出的电场电流有关，比较每个子域在前后迭代得到的电场电流的值，当满足式（2.2.13）的收敛条件时完成方程的求解。
收敛条件为：
                 (2.2.13)
Error一般设置为0.01。
可以看出，区域分解法可以通过将一个大区域分解为若干小区域独立求解进而减少了求解未知量，简化了计算，适用于并行计算。而且对于周期结构，只需对其中几个典型子域进行分析，就可根据结构的周期性得到整体方程的解。
2.3  有限元区域分解法分析具有周期结构的微带阵列天线
区域分解法可以分为分界面的法向量沿一个方向的区域分解法和分界面的法向量沿两个方向的区域分解法[17]。一个方向的区域分解法比较简单，每个子域最多也只能有两个相邻子域，但是这样也就只能分析细长的模型，如圆柱，长方体等。而两个方向的区域分解法分区时更加灵活，也就更适合分解电大尺寸目标，尤其是周期结构，如天线阵。考虑到具有相同结构和边界条件的子域具有相同的系数矩阵，所以对于具有周期结构的天线阵列，我们只需找到其典型子域，计算出典型子域的系数矩阵，就可以根据结构重复性得到其他子域的系数矩阵[18]。
对于沿一个方向分区的周期结构微带阵列有三个典型子域，而对于沿两个方向分区的周期结构微带阵列有九个典型子域，如下图2.2所示：
 
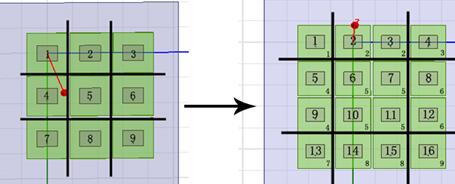
图2.2  微带阵列天线的周期扩展
本节我们研究两个方向的区域分解法，用图2.2中箭头左边 微带阵列的九个典型子域来模拟得到箭头右边 微带阵列中的16个子域。
首先将子域标号如图2.2中所示。其中典型子域中的1、3、7、9位于四个边角不能拓展，对应于子域1、4、13、16。子域2、3对应于典型子域2，子域6、7、10、11对应于典型子域5，子域14、15对应于典型子域8，子域5、9对应于典型子域4，子域8、12对应于典型子域6。由此，我们完成了使用9个典型子域模拟16个子域的过程，由于由同一个典型子域扩展得到的子域具有相同的系数矩阵，求解时也只需要对这九个典型子域进行LU分解，然后将分解结果进行三角回代就可以求出整个天线阵列区域的解。 有限元区域分解技术分析阵列天线辐射特性(4):http://www.youerw.com/tongxin/lunwen_11310.html