第二章，介绍了格林函数的基础理论，包括混合位的表示形式，并且研究分层介质的空域与谱域格林函数，将其应用到微带线上。因为空域形式格林函数非常复杂，计算困难，效率低下，并不适合直接计算。与之相比，谱域格林函数相对简单，容易计算，并且两者之间存在傅里叶变换或汉克变换的关系，体现为Sommerfeld积分变换。
第三章，将插值法应用到Sommerfeld积分的计算。由于Sommerfeld积分的快震荡和慢衰减特性，直接计算非常困难，效率极低。为了解决这个问题，我们可以采用插值法来逼近谱域格林函数。插值法较直接计算效率有所提高，受到了比较多的关注。插值法经过多年发展，派生了很多种类，相关的理论也有很多。我们只是选取了最简单的插值方法，有多项式插值法，Hermite插值法和样条插值。三种方法各有优缺点，计算速度不同，所需条件不同，计算精度也不同。应用到实际中时，我们可以通过对实际问题进行分析来选取究竟使用哪一种插值法。某些时候条件限定时，我们的选择余地就会变的很小，这时我们只能实际根据情况选取最有利的办法。
第四章，就格林函数与插值法的结合举例并且做了数值分析。我们对直接计算格林函数与使用插值法计算举例演算，并进行数值分析。然而插值法也会存在一些问题，比如某些奇异点会无法处理，可以通过原函数分离奇异项的方法进行插值，或者直接将奇异项减去，先对非奇异项进行插值计算。限于篇幅，本文只做粗浅的探讨。
2 格林函数
2.1前言
分层介质的电磁分析方法在远程遥感、地质探测和多层印刷电路中应用广泛。一般的平面分层介质模型如图2.1。它由N+1层不同介质组成，每一层的电导率、磁导率和介电常数都不相同。由于顶层和底层介质的电导率不同，其结构和应用因此也不相同。若 与 均为0，那么图2.1表示全开放结构，此结构在地质探测和介质板模型中均有应用；若 为0， 为正无穷大，那么图2.1表示半开放半封闭结构，此结构在微带模型中经常使用；若 与 为正无穷大，那么图2.1表示全封闭导波结构，它的上下表面被理想导体覆盖，此结构既可以用来描述LTCC技术，也可以用来描述芯片封装中的多层印刷电路。
 
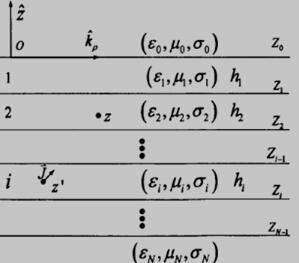
图2.1  平面分层介质的一般结构的示意图
电流是通过并矢格林函数向空间中的任意点传递场的。因为分层介质并矢格林函数包含了分层结构的所有边界条件，所以分层介质中的积分方程与自由空间相比具有统一的形式[6]。但是，分层介质的并矢格林函数形式复杂，不利于数值计算。在矩量法中，我们使用的空域并矢格林函数是由它的谱域表达式经过傅里叶逆变换或Sommerfeld积分求得的[7]。由于Sommerfeld积分中的贝塞尔函数或汉克函数固有的高振荡和慢衰减特性，对于空域表达式的数值计算往往要耗费很多时间[8]。为了克服这个困难，人们进行了很多探索和研究。本章从分层介质的并矢格林函数的基础理论出发[9]，推导了它的空域和谱域表达式，并将其应用到微带线中。 在格林函数求解中的多维插值技术(3):http://www.youerw.com/tongxin/lunwen_21979.html