如图2.2-2所示，空间目标的轨道参数和其它的物理量的关系可根据轨道计算出。
                  图2.2 椭圆几何和轨道参数
r代表目标对于地球中心位置的矢量，r表示的是幅值的大小；V目标对于地球中心的相对速度矢量，v表示的速度矢量的大小；φ是垂直于位置矢量的直线和速度矢量的夹角，叫飞行角或者为航迹角；b是椭圆的半短轴，a是椭圆的半长轴；c是椭圆的一个焦点到中心的距离；θ是顺着目标的运动方向度量的，目标的位置矢量r和地心O到近地点P´矢量之间的夹角，叫做极角，或者是椭圆的真近点角；ra是远地点（椭圆轨道上到地心的距离最远的点）A到地球中心的距离；rp是近地点（椭圆轨道上距离地球中心最近的点）P´到地球中心的距离；e=c/a,是椭圆的偏心率。
目标绕地球飞行时，在r位置矢量处受到的引力为
                                                     （2.2.1）
F是引力的大小，M是地球的质量，G是引力常数。引力矢量表示为
                           r                     （2.2.2）
由牛顿第二定律有：
                                                       (2.2.3)
     是目标的加速度矢量
                           （2.23）
联立可得：
                             （2.24）
θ是极角，e是偏心率，a是半长轴。在a、e一定时，r只是θ的函数。
2.3 轨道要素
轨道要素又称为轨道根数，指的是，在地心轨道系统中，为了确定目标的椭圆轨道所需要的基本常数。确定目标的椭圆轨道需要知道它的形状、大小以及在空间中的位置，有时也需要加上计算运动时间的所需要的的起算点，因此，一共需要6个参数。只要这6个参数确定了，也就确定了目标的运动轨道。这些参数是如图2.3-1轨道的半长轴和轨道的偏心率，轨道倾角、升交点赤经，近地点的幅角和经过近地点时的时刻。
 
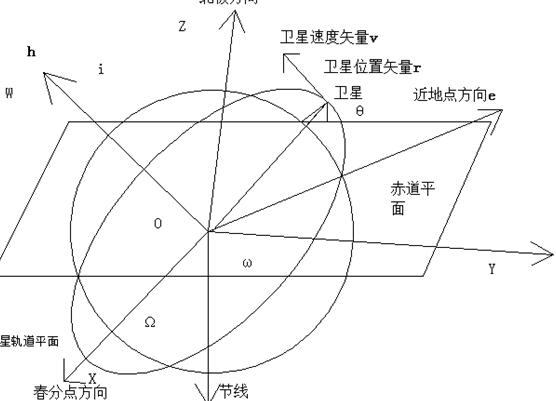
 图2.3 轨道要素的位置关系
轨道半长轴a是指椭圆轨道的长轴的一半；轨道偏心率e描述了轨道的形状和包围面积的大小，它是椭圆焦距和长轴的比值。轨道倾角i是轨道平面的法线和地球轴线的北极方向的夹角，即地球的赤道平面和目标运动的轨道平面的夹角。它用来刻画目标运行的方向，如：在0<i<900时，这表示目标的运动方向和地球的自转方向相同，都是从西向东的或者从西北向东南，在900<i<1800,目标的运动方向和地球的自转方向相反，i=900时，目标轨道经过地球的南北两极。 matlab多部件空间目标红外光谱特性分析(4):http://www.youerw.com/wuli/lunwen_18067.html