电学系统和热学系统之间的关系可以用数学形式表示：
其中:  是节点i 的电压,  是器件j 的温度,  是流入节点m 的电流,     是器件n的热流量,电热耦合模拟,就是在考虑电路自热效应的情况下模拟电路自身功耗造成的工作温度升高和在该温度下的电路性能电热耦合模拟[4]。
1.2  电热耦合简介
电热耦合模拟,就是在考虑电路自热效应的情况下模拟电路自身功耗造成的工作温度升高和在该温度下的电路性能电热耦合模拟[4]。求解非线性方程通常有两种方法， 解耦法(又称Gummel法)和耦合法(又称全Newton法)，根据电热耦合模拟的特点,还有两种新的算法， 组解耦( group Gummel)法和异时间步长( different time-step)法[2]。耦合法是将热的问题映射到电学方程中并且由模拟器同时求解热学和电学子系统， 解耦法是由热学模拟器和电学模拟器分别模拟两个子系统,进行迭代求解[4]。金属无论在室温或更高的温度，它的电阻率都随温度增加[15]。
解决耦合类问题可以通过数值差分方法先将微分方程转化为代数方程再进行求解，对于复杂的热传导问题,仅仅通过理论计算往往难以实现,需要通过数值方法进行求解，本文可以采用有限差分离散方法,对半导体硅芯片表面焊线进行热学分析[13]。目前, 差分方法分为显式方法和隐式方法2 种，相比较而言, 显式方法实现简单, 适合于代数微分方程组的交替求解格式, 但对步长反映比较敏感, 也存在交接误差问题[9]。
1.3  研究现状
1.4  本文研究内容
本文中的模型如图1.1所示：接合线用于连接芯片和基板。当施加电流时，接合线将会产生热量，同时，热量将被释放至芯片表面。这会导致设备的温度升高。建立一文图形来分析施加一定的电流时，接合线的温度分布。在三文模型中，接合线的一部分由一个小正方体表示。

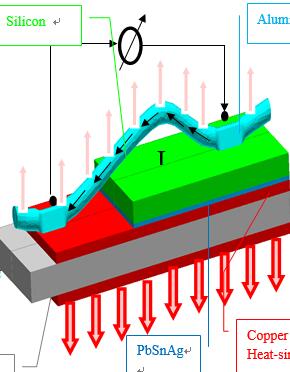
 图1.1 硅芯片和表面焊线模型
接合线的温度分布取决于许多参数（表一）。主要参数有：热通量，横截面积，电阻，导热系数，电流，温度，对流换热系数等。
Parameters    Definitions    Units
    Heat flux at position x    W/m²
    Cross sectional area    m2
    Electrical resistance    Ω
    Electrical current    A
    Perimeter of    m
    Thermal conductivity    W/mK
    Temperature    K
    Electrical resistivity    Ωm
    Heat convection coefficient    W/m²K
                                 表一 所需参数表

在本次研究工作中，本文将分析由电压所引起的电流在一个接合线中的流动以及通过芯片时进行一次电-热模拟功耗加热。在本装置中，各种降温方法都适用于电子元器件。在本次的分析中，本文将主要处理水冷却并研究其对接合线及芯片的温度分布的影响。同时，本文将研究切换瞬态分析开启和关闭按钮时的循环状况。仿真结果和冷却条件有着不可或缺的联系，如对装置进行水冷将导致温度分布极其不均匀，如：接合线处将出现最高温度，而离热源较远处的温度则接近环境温度。在进行仿真模拟时，本文将设置装置外表面与空气间的对流系数为0.8•10-5 W/(mm²•K)来模拟散热。在实验中，本文把底部铜层处的对流系数设置为0.5•10-2 W/(mm²•K)并用它来来模拟水冷的环境，并将环境温度设置为20℃。本研究中模型总共有着有两种完全不同的热输入方式：一种为硅芯片本身产生的热量还有一种为接合线由电流产生热量传导至芯片。 硅芯片表面焊线的电热耦合数值模拟(2):http://www.youerw.com/wuli/lunwen_19025.html