4.2.1  代码改进OMP算法与原始OMP算法对比13
  4.2.2  parfor改进OMP算法与原始OMP算法对比14
  4.3  对比实验结论总结16
  4.4  本章小结18
  结论  19
  致谢 20
  参考文献21
  附录A  代码改进后OMP算法的完整MATLAB代码22
  附录B  parfor改进后OMP算法的完整MATLAB代码23
  图1.1  奈奎斯特采样框架图1
  图1.2  压缩感知采样矩阵框架图1
  图1.3  spams工具箱编译测试结果截图4
  图2.1  第t次迭代过程示意图7
  图3.1  CPU使用情况11
  图4.1  代码改进OMP算法的稀疏系数矩阵14
  图4.2  原始OMP算法得到的稀疏系数矩阵15
  图4.3  实验一仅改变字典大小时代码改进后OMP算法的加速比18
  图4.4  实验二仅改变样本大小时代码改进后OMP算法的加速比18
  图4.5  实验三仅改变迭代次数时代码改进后OMP算法的加速比19
  图4.6  实验四仅改变字典大小时parfor改进和双重改进后OMP算法的加速比19
  图4.7  实验五仅改变样本大小时parfor改进和双重改进后OMP算法的加速比19
  图4.8  实验优尔仅改变迭代次数时parfor改进和双重改进后OMP算法的加速比20
  表4.1  仅改变字典D的大小时算法的加速情况15
  表4.2  仅改变样本X的大小时算法的加速情况16
  表4.3  仅改变迭代次数L的大小时算法的加速情况16
  表4.4  仅改变字典D的大小时算法的加速情况17
  表4.5  仅改变样本X的大小时算法的加速情况17
  表4.6  仅改变迭代次数L的大小时算法的加速情况18
1  绪论
1.1  压缩感知概述
当今飞速的社会发展使人们对信息的需求量逐渐增多，这样就对信息的采集，传输和存储有了更高的要求[14]。并且对采集到的信息需要剔除冗余数据，因此需要一个有效的方法来提取有用信息。压缩感知（Compressed sensing，简称CS），也被称为压缩采样(Compressive sampling)，稀疏采样(Sparse sampling），压缩传感[1]。这个新兴的采样理论，它主要通过研究信号的稀疏特性，在突破传统奈奎斯特（Nyquist）定理的条件下，信号的离散样本通过随机采样获取，信号的重建恢复是通过非线性重建算法来完成[2]。这一过程同时实现了信息采样和压缩，并且能够节省大量存储空间。以下图1.1和图1.2是奈奎斯特采样框架图和压缩感知采样框架图：
 
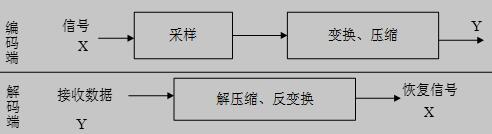
图1.1 奈奎斯特采样框架图
图1.2 压缩感知采样矩阵框架图
压缩感知理论提出之后，就引起了研究人员的广泛关注[3]。他在模式识别、信息论、图像处理、光学微波成像、地球科学、无线通信等领域受到高度关注[4]。压缩感知目前主要研究观测矩阵的设计，信号的稀疏表示，以及恢复信号的重构算法几个方面[5]。其中重构压缩采样后的信号这一方面引起了很多学者的研究，提出了一些算法用于信号恢复，本课题主要就是对其中的OMP算法进行并行优化的研究。
1.2  信号重构算法概述
上节已经对压缩感知做了概述，压缩感知的关键内容是信号重构算法。本节主要简单介绍一下信号重构算法的发展现状。
信号重构算法主要包括匹配追踪类算法、最小化 范数算法、迭代阙值算法、梯度类算法等。这些算法的研究有较强的实用性，是压缩感知中用的比较多的重构算法。 MATLAB稀疏重建OMP算法的并行优化(2):http://www.youerw.com/jisuanji/lunwen_26464.html