时频或时间尺度表示越来越广泛用于对非平稳信号的分析。他们把一个一文信号 的映射到一个二文函数的时间和频率 或时间和规模 TSR,以提取相关的信息。其中,谱图可能是最早的一种，并且仍然是最常用的一种。然而,谱图有严重的缺陷,从理论上讲,因为它提供的信号的瞬时频率和群时延有偏差，并且在实际上，,由Gabor-Heisenberg不平等造成时间和光谱之间的权衡是不可避免的。其他非平稳信号表示方法被提出，用来克服这些显著的缺点，像科恩的类的双线性时频能量分布函数。Wigner-Ville 分布，Margeau-Hill 分布，他们的平滑版本与其他减少交叉项的是同一类。几乎与此同时,一些作者基于尺度而不是频率的概念提出了其他时变信号分析工具,比如量图(平方小波变换模量)仿射平滑伪或损失分布伯特兰分布。这些理论的提出和在这方面领域各种存在方法的运用是确定而且广泛传播的。然而,可读性是这些方法的一个关键要素,这意着不仅需要一个好的信号分量的聚集，也要没有误导的干扰项。这一特点对一个简单的视觉判读的结果和已知对于非平稳的信号分类任务模式之间的一个良好的判别是必需的。为了有一个合适的的可读性,首先必须选择一个干涉几何匹配信号结构的表示方法，然后正确地调整其参数,经验(信号的一些先验知识)或使用自动程序。但通过一个适当的处理更有可能进一步提高表示方法的可读性。这个方法理论最近被不同的学者提出。其中一些提出将信号分解为基本分量并且使用它们的总和来表示信号。其他人通过使用图像处理技术来执行修改信号表示的方法。但这也和Kodera Gendrin,de Villedary 15年前提出的改进移动窗口法目标一样。他们提出了一个灵活修改的谱图,这很遗憾这个方法仍未使用，因为它的效率并没有在理论上证明，所以实现困难。
本文通过他们的算法，即被称为重排的方法，来处理分析微多普勒效应的仿真模型，并且根据算法仿真后的目标微多普勒特性来找出最优算法。
   2  微多普勒效应的研究
2.1 微多普勒效分析
 雷达探测目标时发射机向目标发射电磁波，然后雷达的接收机接收目标反射的的回波信号，这个信号包含了目标的许多信息。而且当目标的运动速度恒定不变时，回波信号的载频会发生偏移，这种现象被称为多普勒频移。多普勒频移现象被广泛的运用于各种雷达当中，它是由雷达发射的电磁波和目标与雷达的相对速度所决定的，fd=2V/ ,V指的是目标与雷达之间的相对速度， 表示的是雷达发射的电磁波的波长。如果目标主方向上的运动速度是恒定不变的，那么因为该恒定的速度所产生的频率偏移也是不会随着时间变化的。如果目标存在旋转和振动，那么它们所引起的频率偏移是一个时变的函数，这种现象称为微多普勒效应。微多普勒效应可以利用数学和物理学的角度进行详细的阐述。在本章接下来的内容里，我们可以通过建立数学模型的方法来分析微运动的微多普勒效应。
    将微运动引入到常规的多普勒分析当中，我们能够导出微多普勒数学的分析方法。为了使分析简单，首先将雷达目标表示为一组点散射，这些点散射就是目标上的主反射点。点散射的模型虽然简化了分析，但是对目标的微多普特性是没有影响的。另外，在简化的模型里，散射体是被看成完美的反射镜，它能够反射拦截的所有能量。
接下来我们可以分析下图的模型：
 
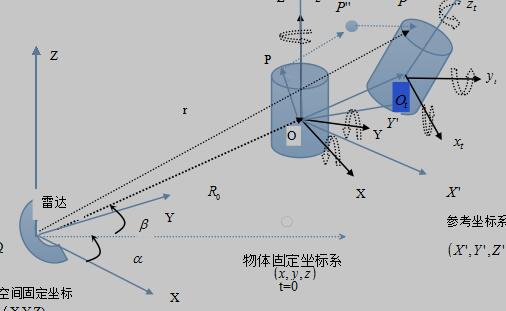
图2.1微运动目标模型 MATLAB基于时频重排技术的目标微多普勒特性研究(3):http://www.youerw.com/tongxin/lunwen_18884.html