1.3  本论文研究的目的和主要内容
由于PID控制器具有优秀的控制性能，并且结构简单、使用方便，在工业控制中的应用已经极为广泛，但是常规PID控制系统是一种线性定常系统，对于一些时变系统和非线性系统就显得无能为力。而模糊控制可以不依赖被控对象精确的数学模型[1]，与PID控制器配合使用，可以根据输出量对PID控制器的参数进行在线整定，修改PID控制器的三个参数使其与输出文持一定的对应关系，这样就弥补了普通的PID控制器对时变系统或者非线性系统控制的不足。因此，在本课题中，主要是以模糊控制为背景，使用MATLAB中的Simulink功能模块和模糊工具箱（fis）建立模糊控制器的仿真模型。以二阶带延时的非线性系统为研究对象，实现PID控制器的模糊在线自整定，并对其进行仿真分析，分别观察两种控制系统的阶跃响应曲线，比较它们的响应特性之间的差异。然后引入阶跃干扰和延迟干扰，观察这两种控制方法干扰后回复稳定的时间，比较它们的抗干扰能力。
2  控制器的基本原理
2.1  常规PID控制器
PID控制器的基本原理如图2.1：
 
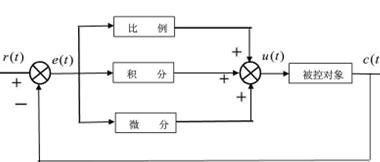
图2.1  PID控制器的基本原理框图
PID控制系统是一种线性的，参数一经设定就恒定不变的控制系统，它利用设定值 与真实输出值 构成偏差
                         2.1
并将偏差 进行比例、积分和微分作用后直接求和得到控制器输出值 。在连续时间域里，PID控制系统的数学表达式如下：
       2.2
式中： 为比例环节，参数 为比例常数；
 为积分环节，参数 为积分时间常数；
 为微分环节， 为微分时间常数。
PID控制器各环节的作用：
①比例环节：引入偏差信号 的成比例控制信号，加速系统响应，缩短调节时间。比例调节的强度与比例常数 密切相关， 越大系统的响应就会越快，调节时间越短，但是会使超调严重，甚至造成系统的不稳定，反之系统响应就会越慢，调节时间越长，如果 过小，控制系统的调节精度就会降低，系统的动、静态特性也会变的十分糟糕，不能形成有效的控制。
②积分环节：引入偏差信号 的在过去很小一段时间的总和，然后成比例的进行调节，这样就消除了系统的静态误差，使PID控制系统的输出值 的稳态值和设定值 保持相同。积分作用的强度与积分时间常数 有关， 越大，系统的积分作用就会越弱， 越小，系统的积分作用则越强。
③微分环节：微分作用是表示响应曲线的斜率，可以判断响应曲线的走势，对偏差信号的变化进行预测，并提前加入一个纠正信号，加快向设定值方向靠拢的速度，提高系统的响应速度，缩短调节时间。
现代计算机控制是一种数字控制系统，数字控制系统也即是一种采样控制，因此PID控制器在连续时间域中的数学表达式(2.2)中的积分项和微分项不能直接应用。首先要使其离散化，利用计算机控制的采样周期T，在一个很短的时间内采取样本值，然后用这些样本值的和来代替这段时间的积分作用，用它们的差来代表这段时间的微分作用，作出如下的变换：
其中T为系统的采样周期。
对于计算机来说，采样周期T一般是个常数，为了书写上的方便，可以省去上式中的采样周期T，将上述式子中 写成  ， 写成 。那么在连续时间域上的数学表达式将变成如下离散时间域上的数学表达式：式子中： 是比例系统； 是积分系统，并且 ； 是微分系数，并且 ； 为系统第k次采样所得的系统输出值； 是系统第k次采样时得到输入系统的偏差值； 是系统第（k-1）次采样时得到的输入系统的偏差值；T是系统的采样周期。 基于MATLAB模糊自整定PID控制器的设计(3):http://www.youerw.com/zidonghua/lunwen_10391.html