（6）对算法的实验结果进行分析，得出不同光学参数和不同入射点对光子传输的影响。
2  基础理论
2.1  光传输的理论模型
研究光在组织中的传输的方法分为两种，一种是基于波动方程的解析理论，该理论考虑了光的波动性，考虑到了光波的衍射、偏振和干涉等波动特征，是严格的传输理论，但因为计算量过大的原因无法得到精确解。另一种是基于中子传输理论的输运理论，该理论忽略光波的偏振和干涉现象，只考虑光的粒子性，追踪介质中光能量的传输，将光的传播看作是粒子在介质中的运动，运动过程中会发生反射、散射和折射等现象，光子与介质的相互作用可由折射率、吸收系数、散射系数和各向异性因子计算得出[3]。
在输运理论中，求解辐射传输方程的难度很大，不适合做高数量级的计算，因此出现了简化的漫射近似理论，但漫射近视理论也有着局限性，只能在某些场景下得到较为精确的解。应用蒙特卡洛方法模拟组织中光传输的过程很好的解决了上述两种理论的不足，得到的模拟结果和实际测量结果基本吻合，该方法的可行性已被光学实验证明并已成功应用到光在组织中传输的仿真问题中，已经成为了一种非光学实验的检验标准[4]。下文就蒙特卡洛方法在生物组织中光子传输仿真中的理论和应用展开论述。
2.2  光在组织中的传输
2.2.1  四个基本光学参数
光子在组织中的传输主要受四个基本光学参数的影响：
（1）µ_a 吸收系数，主要影响组织对光的吸收作用，光子传播一定的距离后权重因此而减小。
（2）µ_s 散射系数，主要影响组织对光的散射作用，发生散射后光的传播方向发生改变。
（3）n 平均折射率，主要影响光在不同介质的交界面发生反射的几率和折射时的偏转角。
（4）g 各向异性因子，又称为平均散射余弦，主要影响光子发生散射时的散射角。g的范围是[-1,1]，g=-1时散射方向的平均余弦值为-1，表示平均散射角为π，即向后散射；g=0时平均散射角为0.5π，即朝各个方向散射的几率是相等的；g=1时平均散射角为0，表示完全向前散射。一般组织的g值在0.8至0.95之间，主要是向前散射。
 
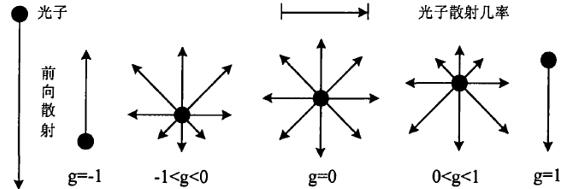
图1 各向异性因子与散射几率的关系
2.2.2  光与组织的相互作用
   一束光照射在生物组织表面可以看作是无数个光子从组织表面出发，由于组织折射率和空气折射率不相等，会产生反射或者折射。光子在组织内部可能发生散射和吸收，经过一系列的散射后光子可能再次运动到组织表面，此时可能发生反射或者折射，反射后重新回到组织内部，直到被吸收或者在组织表面发生折射逃逸出组织。最后所有光子要么被吸收，要么逃逸出组织。
 图2 光子与组织的相互作用
蒙特卡洛方法
2.3.1  概述
蒙特卡洛方法（Monte Carlo Method，MCM）是以概率论与数理统计理论基础为依据的相当重要的随机计算方法, 依赖于重复随机抽样获得计算结果。它采用伪随机数模拟的随机数来解决许多随机性的计算问题，在使用其他数学方法很难或不可能求解时，蒙特卡洛最能发挥作用。理论上，蒙特卡洛方法可以用来解决任何有概率解释的问题。根据大数定律，随机变量的数学期望能近似的以一些服从该分布的独立样本的试验的平均值（样本期望）来描述。只要计算的样本数量足够多，总能得到在某一区间上一定置信水平的解。蒙特卡洛方法在经济学，工程学，计算物理学，基础学科科研等领域有着相当广泛的应用[5]。 光子在苹果中传输的蒙特卡洛仿真+源代码(3):http://www.youerw.com/jisuanji/lunwen_20905.html