MATLAB武装机器人稳定平台随动控制设计(3)
时间:2018-07-07 20:15 来源:毕业论文 作者:毕业论文 点击:次
2.2 基本概念与理论基础 稳定平台的位姿的含义是平台的两轴在惯性空间中的所出位置以及此时的姿态。为了更加的确切表述稳定平台在该空间的位置和姿态,通常情况,在每个坐标轴上建立一个坐标系,这个坐标系成为连体坐标系。开始在空间中确定一个基准坐标系。接着,平台每个转动轴上都需要一个坐标系。因此,上面提到的在空间内表示的连体坐标系原点的位置,就是轴在惯性空间的位置。同样的。姿态由连体坐标系和工作空间所确定。综上,稳定平台运动学的问题可以用坐标系间的转换矩阵来表达出来。 2.2.1 平移变换 图2.1 坐标间的平移移动 假设空间有两个坐标系{A}和{B},这两个坐标系的坐标矢量相互平行,但是原点位置不同。这样我们在空间中找出一点 ,位置坐标可以用矢量代表,因此点P位置坐标可用一个 的矢量 表示,矢量充分表述了坐标的位置点。矢量 。其中, , , 分别可以被称作 在 上的三个坐标位置分量。 在惯性空间中, 容易看出它们的坐标矢量处于平行的状态,同时因为二者的原点位置点不同,在这些因素的作用下,我们就可以认为两个坐标系有一定的联系,联系就是二者是平行的。它们可以互相平移到达对方位置 。如下图2.1所示,点P在坐标系{B}中的坐标为 ,三个矢量 , 和 满足矢量三角形定理,所以点P在坐标系{A}上的坐标 2.2.2 旋转变换 图2.2 坐标的旋转变换 在惯性空间中,设定有两个坐标系 ,二者在空间中重合在一点,这一点称之为原点。但是这两个坐标系的三个坐标轴不处于重叠的状态下。那么它们互相的关系可以称之为旋转关系 。在上图中,我们把 视作为两个坐标系,也就是 ,二者之间的相互变换的联系,也就是在某种条件下,它们的转换。在惯性空间中,设定一点 ,已知该点的坐标 ,代表在 上的位置表示点。同理,该点在 中的位置我们可以表示为 。可以容易的推导出以下等式: 同理,可以由 导出 : (其中 ) 旋转矩阵 也可以用其他形式表示更容易计算, 。在前面的等式中 , , ,设定为分别表示坐标系 以坐标系 的三个坐标轴为基准旋转 , , 角度。所以,计算出以 三个坐标轴 为基准的旋转矩阵是 : 2.2.3 复合变换 如果两个坐标系{A}和{B}的原点不重合,而且两坐标系中坐标轴不互相平行。如图2.2.3所示,点P在坐标轴{A}上的坐标为 ,在坐标轴{B}上的坐标为 ,坐标系{B}相对于坐标系{A}的旋转矩阵为 ,坐标系 中的原点因为和 是不同的,需要假定 原点用 中坐标来表示,该坐标为 。在下图中容易得出坐标系 先按旋转矩阵 旋转到与坐标系 平行的位置,然后在这个位置沿着平移矩阵 平移到与坐标系 重合的地方。惯性空间中的一点 表示在两个坐标系里是不同的 ,可以用 和 标记,它们的关系是: 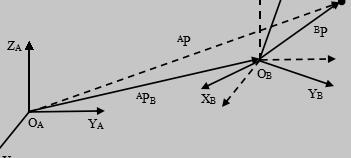 图2.3 坐标的复合变换 2.3 稳定平台运动学方程 2.3.1 稳定平台的构成 图2.4 稳定平台的简化图 本文研究的是武装机器人稳定平台的随动控制,稳定平台有两个自由度,平台在两个方向上有位移,可以用框架来表示,在画框架图时可以用两个相互铰接的框架表示系统的运动。这两个铰接的框架分为绕Y轴转动的框架1(外框架)以及绕X轴转动的框架2(内框架)。利用框架很容易就将稳定平台简化出上图的结构,这个结构清晰地表示出平台运动的过程,为接下来的研究提供了方便。 (责任编辑:qin) |