一维混沌映射系统的分岔与相变研究(2)
时间:2018-07-29 20:40 来源:毕业论文 作者:毕业论文 点击:次
2 一文混沌映射介绍 在很长的一段时间里,人们对既具有确定性又具有随机性的动力学行为理解的并不是很清楚明了。自上世纪60年代以来,人们认识到低文非线性系统由于自身非线性特点也可以产生确定兼具随机的复杂行为[4-7]。因此,本文将从低文混沌系统入手,研究混沌系统在分岔过程中所可能服从的规律。在这里我们主要考虑了一文的Logistic映射与Tent映射系统,本章首先对这两个离散系统的动力学行为做简单介绍。 2.1 Logistic映射 为了研究物种世代繁殖与种族数量之间所表现出来的非线性行为,生物学家May提出了Logistic映射:(2-1) 其中 是模型参数,是根据繁殖和饿死率而得出的相关参数; 代表第 代种群相对最大种群数的比值,满足 。值得注意的是:当种群数量的相对值 时,表示种群灭绝;当 时表示种群数量极盛,这将导致食物枯竭,意着种群即将走上灭绝。故通常考虑 范围内的动力学行为。 Logistic映射是一个离散的迭代方程,常用于描述一个生物种群数量随繁殖代数而变化的情况。 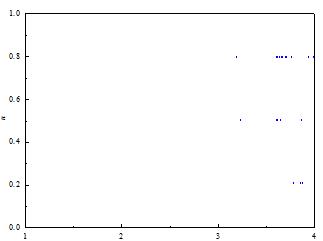 图2-1 Logistic映射分岔图 图2-1给出了Logistic映射 随模型参数 的分岔图。从图可以看出,随着 的增加, 从开始的周期1进入到周期2。继续增加 ,可以看到一系列的倍周期 分岔,系统的周期由2变为4,8, ,一直到 。继续改变 ,系统出现复杂的混沌运动。因此, 是系统从周期行为进入到混沌运动的一个临界点。具体可归纳为: 1) 当 时,对于任意初值 , 都会快速趋于定态区域的不动点 ; 2) 当 时,无论初值如何, 会处在2个状态之间跳跃性循环; 3) 当 之间, 最后会处在4个状态之间持续的周期性震荡; 4) 当 时, 从周期8进入到周期16,32, ,最终系统过渡到无序的混沌运动; 5) 当 , 进入混沌运动。此外,在这个混沌区域中 会经历一系列的非倍周期窗口,也就是分岔图中对应的混沌窗口。 (责任编辑:qin) |