Fluent带尾翼火箭发射气动特性研究(3)
时间:2019-02-19 21:06 来源:毕业论文 作者:毕业论文 点击:次
b)运用ANSYS Workbench软件建立几何模型 c)运用ANSYS ICEM CFD对弹丸外场进行网格划分 d)运用ANSYS Fluent软件进行计算分析外流场 2 数学物理模型 带尾翼弹箭的数学模型是把实际弹丸飞行流场的问题转化为数学问题,并将从数学的角度来描述分析实际流场问题。本文的控制方程采用欧拉方程,该数学模型能够较好的描述弹箭的全流场信息。 2.1 控制方程 牛顿第二定律在运动流体上的应用,在空气动力学中体现为动量方程[8]。动量方程有两种形式,分别是微分形式和积分形式。欧拉方程即为动量方程中微分形式的动量方程,又称为运动方程。欧拉方程就是流体微团所受的力与它的加速度建立起来的关系,它是在不计流体粘性的前提下推导的,下面对欧拉方程进行推导。 在流场中划出一块流体,形状为微元矩形优尔面体,三边长度分别为 ,如下图2.1所示。 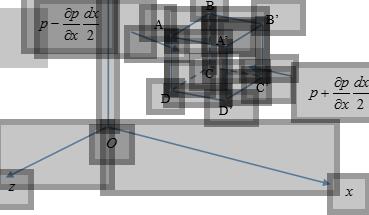 图2.1 欧拉方程推导示意图 这块微团所受的力,在不计粘性力的情况下,表面力就没有切向力,仅仅有法向力一种,也就是压力。彻体力是可以存在的。嘉定微元矩形优尔面体的中心点坐标是 ,词典的流体速度为 ,压强为 ,密度为 。则侧面 中心点的压强为 这也是作用在这个面上的平均压强,所以这个侧面上的压力为 这个力指向 的正方向。同理,作用在另外一个侧面 上的压力为 这个力指向 的负方向。两项相加得 正方向的合力为 其它四个侧面的压力在 方向都没有投影。 假定这块流体的中心点的彻体力的三个分量是 ,这些力是坐标的函数,也都是单位质量的彻体力。 加速度的表达式为 这块流体的质量是 ,按运动第二定律得 向的欧拉方程为 整理并把实导数各项写出来,此式变为 同理, 向和 向的欧拉方程是 (责任编辑:qin) |