(2-1) (2-2)
(2) 傅立叶变换的基本性质
若 = , = ,则
线性性质: (2-3)
坐标缩放性质:
平移性: (2-4)
(3) 傅立叶变换的基本定理
若 = , = ,则
卷积定理: ,
(2-5)
互相关定理:FT{g(x,y)☆h(x,y)}=
自相关定理:FT{g(x,y)☆g(x,y)}=
2.2 阿贝成像和空间滤波
2.2.1 阿贝成像原理
空间滤波的目的是通过在频谱面上有目的性地选取人们感兴趣的部分,使像产生相应的变换,自从1873年阿贝(Able)提出阿贝成像理论之后,空间滤波理论开始受到人们高度重视。阿贝的二次成像过程分为以下两步:第一步是在以输入的物为衍射屏发生夫琅和费衍射;第二步频谱综合过程,即从频谱面到像平面,被分解的频谱成分经进一步的衍射后再次综合形成输入物体的像.按照傅里叶变换理论,两步成像过程实际上是光学系统对携带输入物信息的二文光场的复振幅分布进行的两次傅里叶变换过程[6]。 阿贝成像理论第一次引入频谱的概念,启示了人们可以通过改变频谱信息的手段改造图像,根据阿贝成像理论,成像透镜的后焦面即为物的频谱面,在该面上可以采集到物的傅里叶频谱,如果在频谱面(后焦面)上放置各种挡光物,如狭缝、小圆孔、圆环或小圆屏等,就可以直接改变频谱,从而使像发生相应的变化。在频谱面上放置不同的滤波器时,输出面上像场的变化情况就不同。图2.1是上述成像过程的示意图:
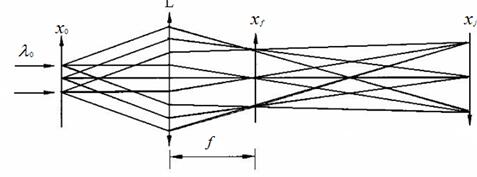
图2.1 4f光学成像系统示意图
物面 用相干平行光照明,在后焦面即频谱面 上得到物的频谱,这是第一次成像过程,实际上是经过了一次傅里叶变换;从频谱面得到像面 实际上是又完成了一次傅里叶变换。经上述两个过程,像面上形成的是物体的像。像面到物面的距离正好是透镜焦距的四倍,因此该系统被称为4f光学成像系统。可以把这样的成像过程看成两步:第一步是信息分解,第二步是信息合成。这就是阿贝二次成像理论,由此启示了人们可以通过改变频谱的手段来改造光学信息[7]。
根据傅里叶理论分析可知,频谱面上的光场分布与物的结构密切相关,原点附近分布着物的低频率信息,即傅里叶低频分量;离原点较远处,分布着物的较高的频率信息,即傅里叶高频分量。根据阿贝二次成像原理,使我们有可能利用空间滤波的方法来改造图像,即通过改造空间频谱继而改变像的信息的手段来满足不同的需要。空间滤波装置采用4f系统(三透镜系统),